スピン拡散方程式を解く

強磁性絶縁体と非磁性金属の二層系 ¶

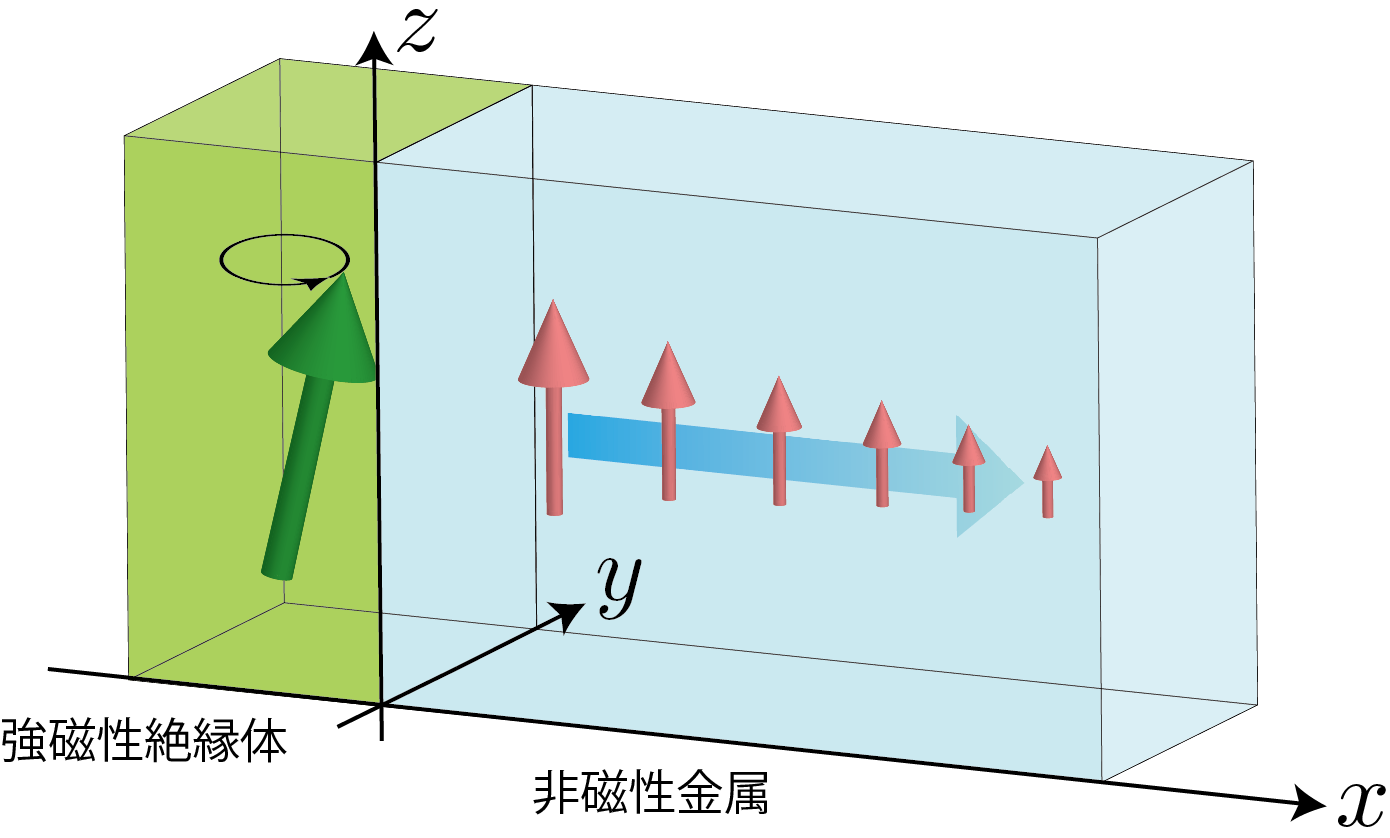
まず，強磁性絶縁体と非磁性金属の二層系を考える． スピンポンピングにより強磁性絶縁体から非磁性金属にスピン流が流れ込む状況を扱う． 流れ込んだスピン流が非磁性金属中においてどのようなスピン蓄積を生じさせるかをスピン拡散方程式に基づいて解析する． ここでは，流れ込むスピン流は接合界面で一定であり，その具体的な表式は与えられているものとして扱う． この仮定から，スピン蓄積は接合界面からの距離のみの関数となり，解くべきスピン拡散方程式は1次元スピン拡散方程式であることが分かる． すなわち， $$\begin{align} \frac{\partial^2 \mu (x)}{\partial x^2} & = \frac{\mu (x)}{\lambda_N^2} \label{eq:SDE_2}\end{align}$$ で与えられる． ここで，$\mu (x)$は非磁性金属のスピン蓄積であり，$\lambda_N$はスピン拡散長である． 強磁性絶縁体と非磁性金属の接合界面を$x = 0$として，$x < 0$に強磁性絶縁体があり，$0 < x < d_N$に非磁性金属があるとする． また，非磁性金属における拡散スピン流は $$\begin{align} j_s (x) & = - \frac{\sigma_N}{e} \frac{\partial \mu (x)}{\partial x}\end{align}$$ で与えられる． ただし，$\sigma_N$は非磁性金属の電気伝導度で，$-e$は電子の電荷である．

式 (\ref{eq:SDE_2})を解く上で，境界条件として以下のものを考える．

1. $x = 0$で，大きさ$j_{s}^{(0)}$のスピン流が非磁性金属に流入している． $$\begin{align} j_s (0) = j_{s}^{(0)} \label{eq:BC1_2}\end{align}$$

2. $x = d_N$では，拡散スピン流はゼロとなる． $$\begin{align} j_s (d_N) = 0 \label{eq:BC2_2}\end{align}$$

スピン拡散方程式 (\ref{eq:SDE_2})の一般解は $$\begin{align} \mu (x) & = A e^{x / \lambda_N} + B e^{- x / \lambda_N}\end{align}$$ となるので，境界条件 (\ref{eq:BC1_2})と(\ref{eq:BC2_2})を満たす$A$と$B$を求める． 計算の詳細を記すと，まず拡散スピン流は $$\begin{align} j_s (x) & = - \frac{\sigma_N}{e \lambda_N} \left( A e^{x / \lambda_N} - B e^{- x / \lambda_N} \right)\end{align}$$ と書けるので，境界条件はそれぞれ $$\begin{align} j_s (0) & = - \frac{\sigma_N}{e \lambda_N} (A - B) = j_s^{(0)} \label{eq:BC1_2-calc}\end{align}$$ $$\begin{align} j_s (d_N) & = - \frac{\sigma_N}{e \lambda_N} \left( A e^{d_N / \lambda_N} - B e^{- d_N / \lambda_N} \right) = 0 \label{eq:BC2_2-calc} .\end{align}$$ ここで式 (\ref{eq:BC2_2-calc})から$B = A e^{2 d_N / \lambda_N}$と分かるので，これを式 (\ref{eq:BC1_2-calc})に代入すると， $$\begin{align} 2 A e^{d_N / \lambda_N} & = \frac{e}{\sigma_N} \frac{j_s^{(0)} \lambda_N}{\sinh \frac{d_N}{\lambda_N}} \label{BC-2}\end{align}$$ となるので， $$\begin{align} \mu (x) & = A e^{d_N / \lambda_N} \left( e^{(x - d_N) / \lambda_N} + e^{- (x - d_N) / \lambda_N} \right) \notag \\ & = 2 A e^{d_N / \lambda_N} \cosh \frac{x - d_N}{\lambda_N} ,\end{align}$$ ここで式 (\ref{BC-2})を代入すれば， $$\begin{align} \mu (x) & = \frac{e}{\sigma_N} j_s^{(0)} \lambda_N \frac{\cosh \frac{x - d_N}{\lambda_N}}{\sinh \frac{d_N}{\lambda_N}}\end{align}$$ を得る．

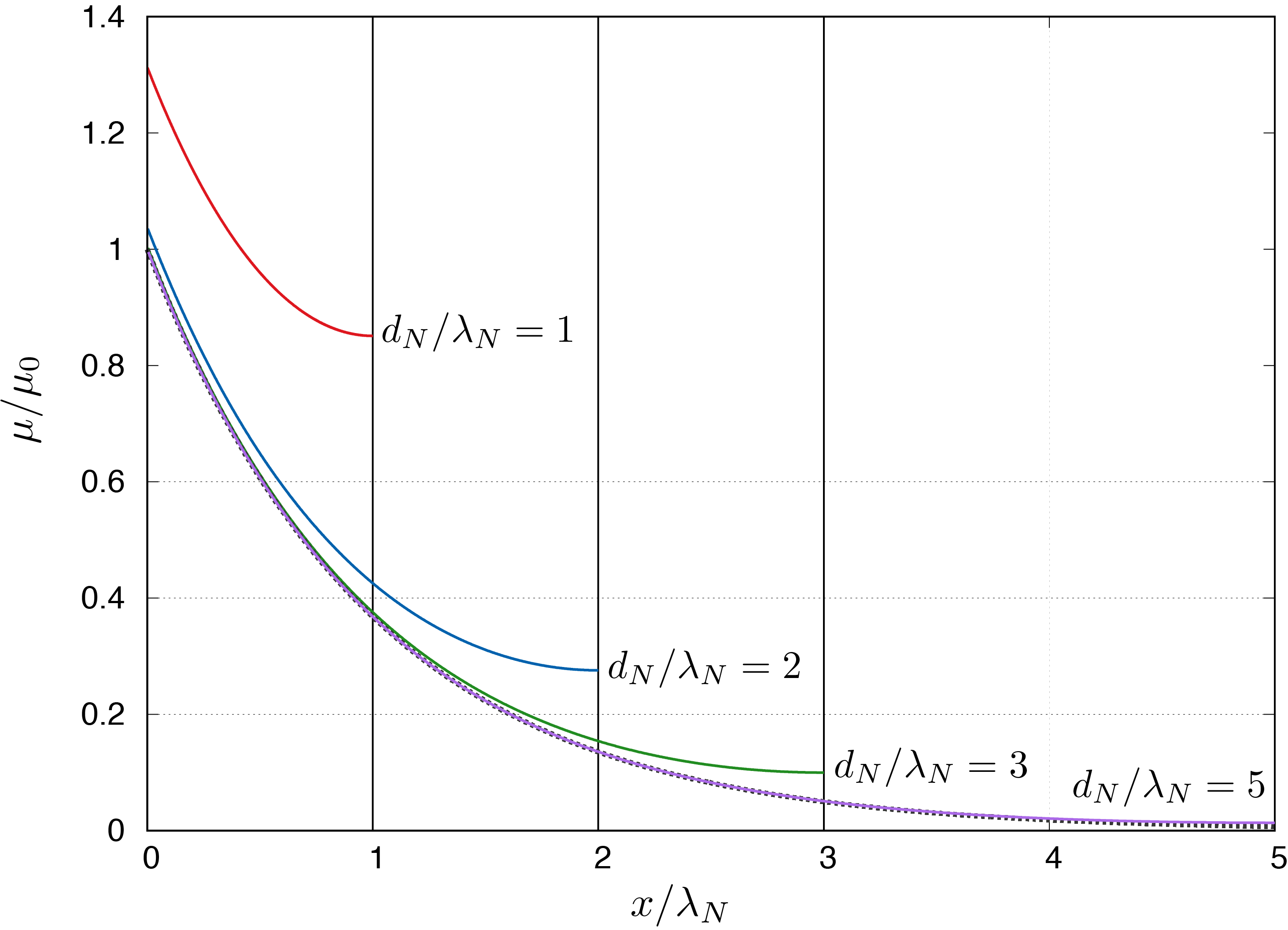
特に，スピン拡散長$\lambda_N$よりも非磁性金属が十分に厚く，$d_N \gg \lambda_N$が満たされている場合， $$\begin{align} \frac{ \cosh \frac{x - d_N}{\lambda_N} }{ \sinh \frac{d_N}{\lambda_N} } & = \frac{ e^{- x / \lambda_N} + e^{(x - 2 d_N) / \lambda_N} }{1 - e^{- 2 d_N / \lambda_N}} \simeq e^{- x / \lambda_N} \label{eq:spin_accumulation_2layer}\end{align}$$ となり，スピン蓄積は界面から遠ざかるほどに指数関数的に減衰していくことが分かる． そこから$d_N$が小さくなるにつれて，$x = d_N$の端にスピンが溜まる影響が生じる（下図）．

強磁性絶縁体と重金属の二層系 ¶

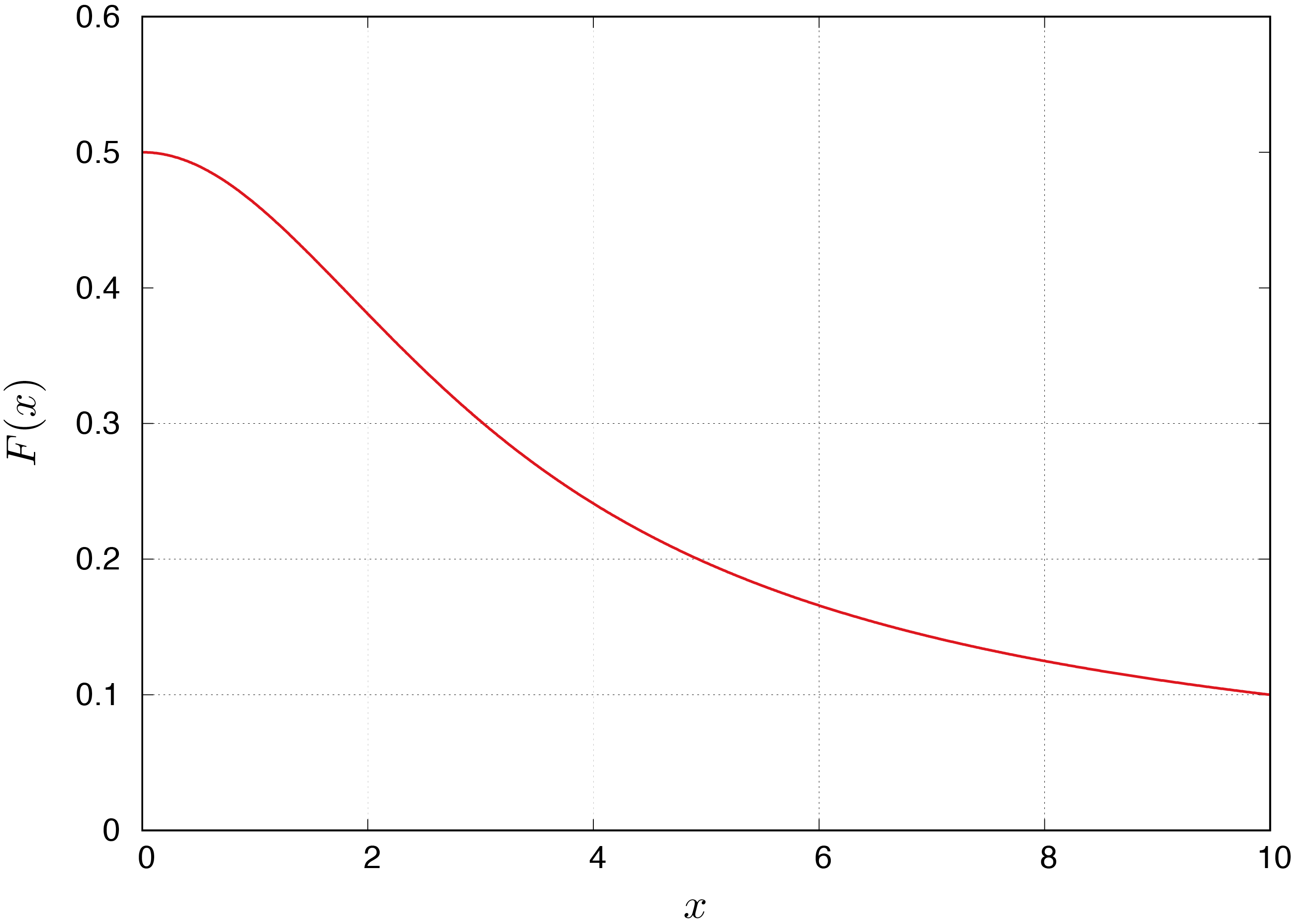
次に，非磁性金属のなかでも，特にスピン軌道相互作用の大きな金属（ここでは重金属と呼ぶ）にした場合を考える． その場合，$z$方向に偏極した拡散スピン流は逆スピンHall効果によって$y$方向の電圧を生じさせる． その変換はスピンHall角を$\theta$とすると，$j_y (x) = - \theta j_s (x)$と書ける． ここで$j_y (x)$は$y$方向の電流である． 厳密には，$y$方向の電圧によって$y$方向の電流が誘起され，それがまたスピンHall効果によって$x$方向のスピン流を誘起するが，その過程は$\theta^2$の寄与なので，無視しても良いだろう． （$\theta \simeq 0.1$としても，$\theta^2 \simeq 0.01$となる．） 結局，重金属の厚みを$d_H$，スピン拡散長を$\lambda_H$，電気伝導度を$\sigma_H$とすると，スピンポンピングによって誘起されるスピン蓄積の分布は，式 (\ref{eq:spin_accumulation_2layer})において$d_N$と$\lambda_N$，$\sigma_N$をそれぞれ$d_H$と$\lambda_H$，$\sigma_H$に置き換えた式で表されることになる． $$\begin{align} \mu (x) & = \frac{e}{\sigma_H} j_s^{(0)} \lambda_H \frac{\cosh \frac{x - d_H}{\lambda_H}}{\sinh \frac{d_H}{\lambda_H}} .\end{align}$$ これから拡散スピン流は $$\begin{align} j_s (x) & = - \frac{\sigma_H}{e} \frac{\partial \mu (x)}{\partial x} = - j_s^{(0)} \frac{\sinh \frac{x - d_H}{\lambda_H}}{\sinh \frac{d_H}{\lambda_H}}\end{align}$$ となり，逆スピンHall効果による電流は，重金属の領域に渡って積算したものが電圧$V_{\text{2layer}}$として測られるとすると，系の幅を$W$とすると， $$\begin{align} \int_0^{d_H} \dd{x} \left( j_y (x) + \sigma_H \frac{V_{\text{2layer}}}{W} \right) = 0\end{align}$$ すなわち， $$\begin{align} V_{\text{2layer}} & = \frac{2 \theta W j_s^{(0)} \lambda_H}{\sigma_H d_H} \frac{ \sinh^2 \frac{d_H}{2 \lambda_H} }{ \sinh \frac{d_H}{\lambda_H} } \equiv \frac{\theta W j_s^{(0)}}{\sigma_H} F (d_H / \lambda_H) ,\end{align}$$ ただし $$\begin{align} F (x) & = \frac{2}{x} \frac{ \sinh^2 (x/2) }{ \sinh x }\end{align}$$ とおいた． $F (x)$をプロットすると，下図のようになる． 特に，$x = d_H / \lambda_H \to 0$の極限を考えると， $$\begin{align} F (x) & \simeq \frac{2}{x} \frac{(x/2)^2}{x} = \frac{1}{2}\end{align}$$ となり，一定値になる． ほんとか？厚みゼロでも電圧は出るということ？

強磁性絶縁体と非磁性金属と重金属の三層系 ¶

最後に，強磁性絶縁体 (FI)と非磁性金属 (NM)と重金属 (HM)の三層系を考える． 座標系は下図のように導入する．

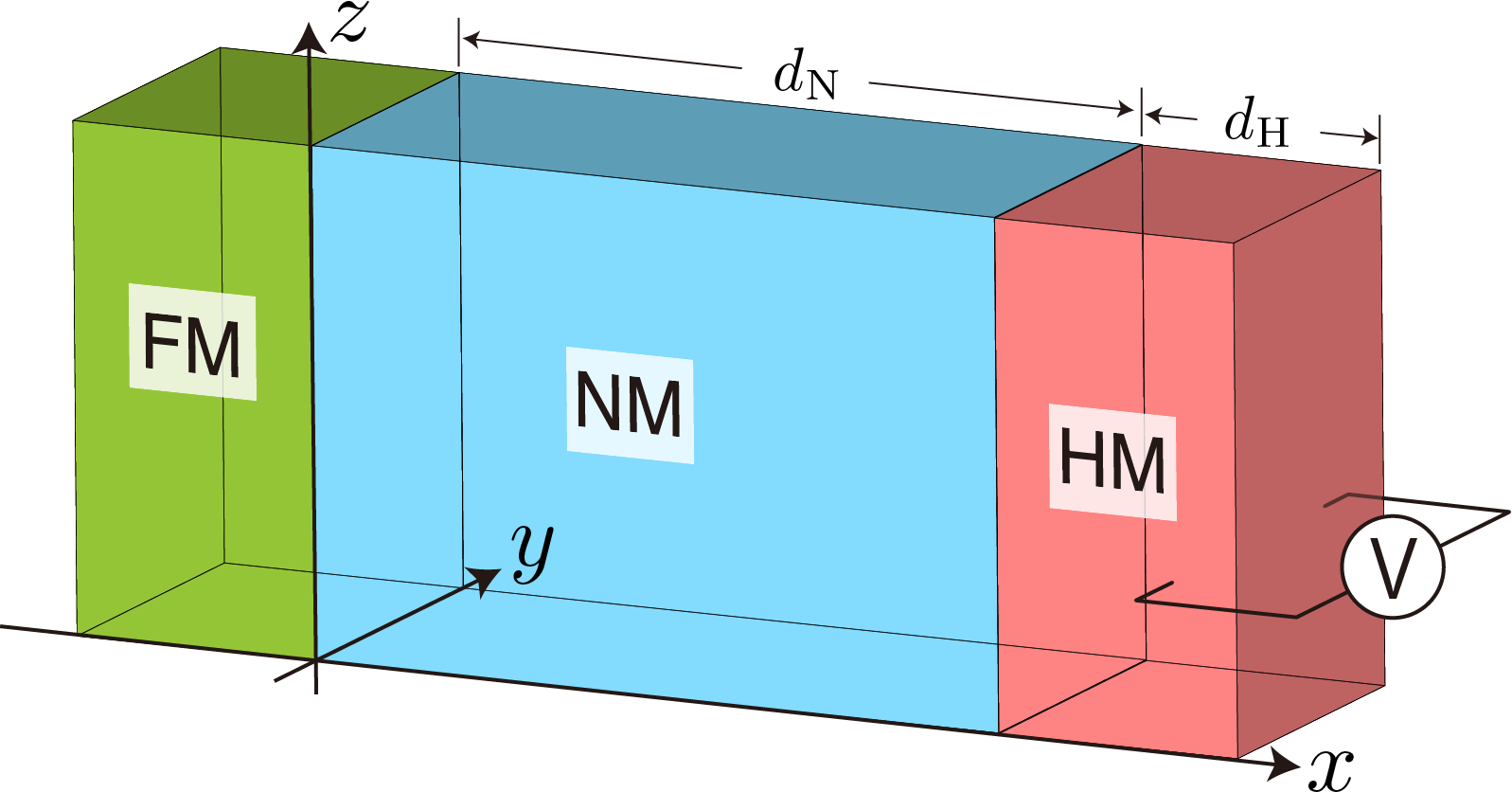
この場合も，仮定として，FI/NM界面に一様にスピン流が注入されているとすることで，解くべきスピン拡散方程式が1次元の微分方程式に落ちる． すなわち，NM層とHM層それぞれのスピン拡散方程式は $$\begin{align} \frac{\partial^2 \mu_N (x)}{\partial x^2} = \frac{\mu_N (x)}{\lambda_N^2} , \qquad \frac{\partial^2 \mu_H (x)}{\partial x^2} = \frac{\mu_H (x)}{\lambda_H^2} \label{eq:SDE_3}\end{align}$$ となる． ただし，$\mu_N (x)$と$\mu_H (x)$はそれぞれNM層とHM層のスピン蓄積である． 拡散スピン流は以下で定義される． $$\begin{align} j_s^N (x) = - \frac{\sigma_N}{e} \frac{\partial \mu_N (x)}{\partial x} , \qquad j_s^H (x) = - \frac{\sigma_H}{e} \frac{\partial \mu_H (x)}{\partial x} \label{eq:spin_current_3layer}\end{align}$$ ここで，境界条件として以下を考える．

1. $x = 0$では大きさ$j_s^{(0)}$のスピン流が流れ込んでいる． $$\begin{align} j_s^N (0) & = j_s^{(0)} \label{eq:BC1_3}\end{align}$$

2. $x = d_N$においてスピン蓄積とスピン流は連続に接続される． $$\begin{align} \mu_N (d_N) & = \mu_H (d_N) \label{eq:BC2_3} , \end{align}$$ $$\begin{align} j_s^N (d_N) & = j_s^H (d_N) \label{eq:BC3_3}\end{align}$$

3. $x = d_N + d_H$の端においてスピン流はゼロとなる． $$\begin{align} j_s^H (d_N + d_H) & = 0 \label{eq:BC4_3}\end{align}$$

スピン拡散方程式 (\ref{eq:SDE_3})の一般解は $$\begin{align} \mu_N (x) = A e^{x / \lambda_N} + B e^{- x / \lambda_N} , \qquad \mu_H (x) = C e^{x / \lambda_H} + D e^{- x / \lambda_H}\end{align}$$ なので，境界条件を満たすように$A, B, C, D$を決めていく． まず，境界条件 (\ref{eq:BC4_3})から，$D = C e^{2 d / \lambda_H}$であることが分かる． ただし$d = d_N + d_H$とおいた． これから， $$\begin{align} \mu_H (x) & = 2 C e^{d / \lambda_H} \cosh \frac{x - d}{\lambda_H} , \\ j_s^H (x) & = - \frac{\sigma_H}{e \lambda_H} 2 C e^{d / \lambda_H} \sinh \frac{x - d}{\lambda_H}\end{align}$$ と書けるので，境界条件 (\ref{eq:BC2_3})は， $$\begin{align} A e^{d_N / \lambda_N} + B e^{- d_N / \lambda_N} & = 2 C e^{d / \lambda_H} \cosh \frac{d_H}{\lambda_H} \label{eq:BC2_3-calc} ,\end{align}$$ また，境界条件 (\ref{eq:BC3_3})は $$\begin{align} & - \frac{\sigma_N}{e \lambda_N} \left( A e^{d_N / \lambda_N} - B e^{- d_N / \lambda_N} \right) = - \frac{\sigma_H}{e \lambda_H} 2 C e^{d / \lambda_H} \sinh \frac{- d_H}{\lambda_H} \notag \\ & \therefore,, A e^{d_N / \lambda_N} - B e^{- d_N / \lambda_N} = - \frac{\sigma_H}{\sigma_N} \frac{\lambda_N}{\lambda_H} 2 C e^{d / \lambda_H} \sinh \frac{d_H}{\lambda_H} \label{eq:BC3_3-calc} .\end{align}$$ よって，式 (\ref{eq:BC2_3-calc})と(\ref{eq:BC3_3-calc})の和と差から， $$\begin{align} A e^{d_N / \lambda_N} & = C e^{d / \lambda_H} \left( \cosh \frac{d_H}{\lambda_H} - \frac{\sigma_H}{\sigma_N} \frac{\lambda_N}{\lambda_H} \sinh \frac{d_H}{\lambda_H} \right) , \\ B e^{- d_N / \lambda_N} & = C e^{d / \lambda_H} \left( \cosh \frac{d_H}{\lambda_H} + \frac{\sigma_H}{\sigma_N} \frac{\lambda_N}{\lambda_H} \sinh \frac{d_H}{\lambda_H} \right)\end{align}$$ を得る． これを境界条件 (\ref{eq:BC1_3})に代入すると， $$\begin{align} C e^{d / \lambda_H} & = \frac{e j_s^{(0)}}{2} \frac{1}{ \frac{\sigma_N}{\lambda_N} \sinh \frac{d_N}{\lambda_N} \cosh \frac{d_H}{\lambda_H} + \frac{\sigma_H}{\lambda_H} \cosh \frac{d_N}{\lambda_N} \sinh \frac{d_H}{\lambda_H} }\end{align}$$ と解けて，結局， $$\begin{align} \mu_N (x) & = A e^{d_N / \lambda_N} e^{(x-\lambda_N) / \lambda_N} + B e^{- d_N / \lambda_N} e^{- (x - d_N) / \lambda_N} \notag \\ & = \frac{e}{\sigma_N} j_s^{(0)} \lambda_N \frac{ \frac{\sigma_N}{\lambda_N} \cosh \frac{x - d_N}{\lambda_N} \cosh \frac{d_H}{\lambda_H} - \frac{\sigma_H}{\lambda_H} \sinh \frac{x - d_N}{\lambda_N} \sinh \frac{d_H}{\lambda_H} }{ \frac{\sigma_N}{\lambda_N} \sinh \frac{d_N}{\lambda_N} \cosh \frac{d_H}{\lambda_H} + \frac{\sigma_H}{\lambda_H} \cosh \frac{d_N}{\lambda_N} \sinh \frac{d_H}{\lambda_H} } \label{eq:spin_accumulation_N_3}\end{align}$$ また，$d = d_N + d_H$をあらわに書いて， $$\begin{align} \mu_H (x) & = e j_s^{(0)} \frac{ \cosh \frac{x - d_N - d_H}{\lambda_H} }{ \frac{\sigma_N}{\lambda_N} \sinh \frac{d_N}{\lambda_N} \cosh \frac{d_H}{\lambda_H} + \frac{\sigma_H}{\lambda_H} \cosh \frac{d_N}{\lambda_N} \sinh \frac{d_H}{\lambda_H} } \label{eq:spin_accumulation_H_3} .\end{align}$$

確認として，スピン蓄積の式 (\ref{eq:spin_accumulation_N_3})と(\ref{eq:spin_accumulation_H_3})に対して，$\sigma_N = \sigma_H = \sigma$かつ$\lambda_N = \lambda_H = \lambda$とすると， $$\begin{align} \mu_N (x) & = \frac{e}{\sigma} j_s^{(0)} \lambda \frac{ \cosh \frac{d_N}{\lambda} \cosh \frac{d_H}{\lambda} - \sinh \frac{d_N}{\lambda} \sinh \frac{d_H}{\lambda} }{ \sinh \frac{d_N}{\lambda} \cosh \frac{d_H}{\lambda} + \cosh \frac{d_N}{\lambda} \sinh \frac{d_H}{\lambda} } = \frac{e}{\sigma} j_s^{(0)} \lambda \frac{\cosh \frac{x - d_N - d_H}{\lambda}}{\sinh \frac{d_N + d_H}{\lambda}} = \mu_H (x)\end{align}$$ となり，電気伝導度$\sigma$，スピン拡散長$\lambda$で，厚さ$d_N + d_H$の一つの層におけるスピン拡散方程式の解に一致する．

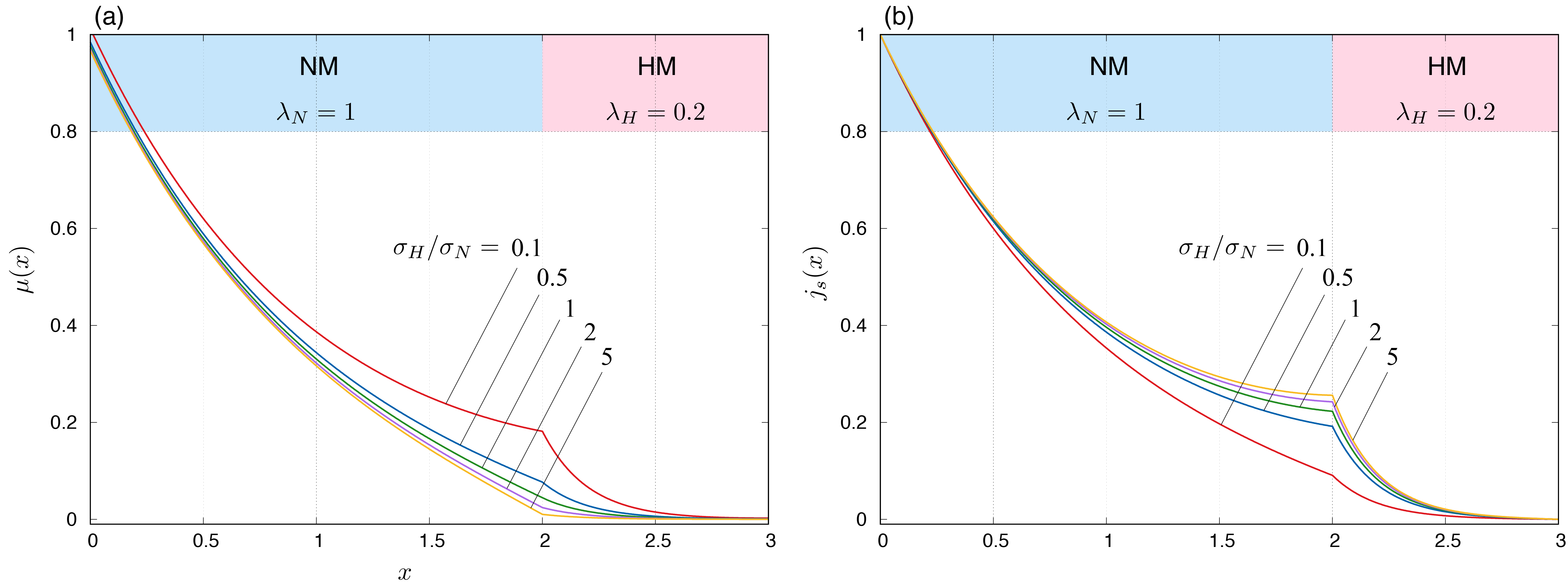
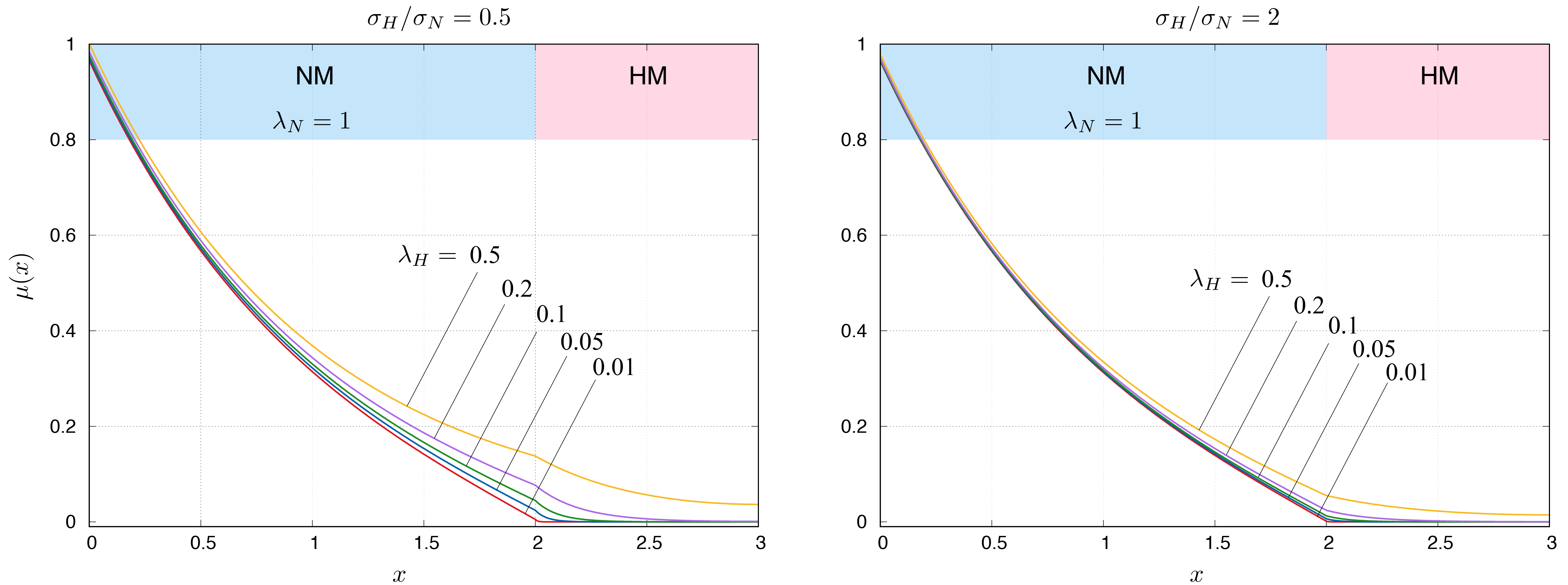
結果をいくつかのパラメタでプロットすると，下図のようになる． 下図において，NMのスピン拡散長を1として，試料の厚みをそれぞれ$d_N = 2$, $d_H = 1$としている点は共通である． 一つ目の図 (a)においてはNMとHMでの電気伝導度の比$\sigma_H / \sigma_N$を変えてスピン蓄積をプロットしている． ここで，注目すべきは，$x = d_N$での境界条件 (\ref{eq:BC3_3})の，スピン流が連続であるという条件である． その条件を少し書き換えると， $$\begin{align} \frac{\partial \mu_N (d_N) / \partial x}{\partial \mu_H (d_N) / \partial x} & = \frac{\sigma_H}{\sigma_N}\end{align}$$ となり，スピン蓄積の勾配の比が，電気伝導度の比で与えられることに等しいことが分かる． 二つ目の図を見ると，（界面でスピン流が連続なので）流入するスピン流は一定であるが，界面でのスピン蓄積の度合いが異なることが言える． 特に$\sigma_H / \sigma_N = 0.1$の場合，すなわちHMの方が1桁電気伝導度が低い場合は，界面のNM側でスピン蓄積が大きく生じていることが見てとれる． 逆に，$\sigma_H / \sigma_N = 5$の場合，すなわちHMの方が5倍電気伝導度が高い場合はほとんどHMにスピン蓄積が生じていない． これに対して，二つ目の図 (b)では，スピン流 (\ref{eq:spin_current_3layer})をプロットしているが，$\sigma_H / \sigma_N$が大きいほどスピン流は多くHMに入り込んでいることが分かる．

逆スピンHall起電力$E_y$を求める． それは $$\begin{align} \int_0^{d_N + d_H} \dd{x} ( j_y (x) + \sigma (x) E_y ) = 0\end{align}$$ から求まる． ただし， $$\begin{align} \sigma (x) & = \left\{ \begin{array}{c c} \sigma_N & (0 < x < d_N) , \\ \sigma_H & (d_N < x < d_N + d_H) \end{array} \right.\end{align}$$ とおいた． HM層のみで逆スピンHall効果が生じているので，結局， $$\begin{align} (\sigma_N d_N + \sigma_H d_H) E_y & = - \int_{d_N}^{d_N + d_H} \dd{x} j_y (x) = \theta \int_{d_N}^{d_N + d_H} \dd{x} j_s^H (x) = - \theta \frac{\sigma_H}{e} \mu_H (x) \Big|_{x=d_N}^{x=d_N+d_H} \end{align}$$ $$\begin{align} & \therefore E_y = \frac{ 2 \theta \sigma_H j_s^{(0)} }{\sigma_N d_N + \sigma_H d_H} \frac{ \sinh^2 \frac{d_H}{2 \lambda_H} }{ \frac{\sigma_N}{\lambda_N} \sinh \frac{d_N}{\lambda_N} \cosh \frac{d_H}{\lambda_H} + \frac{\sigma_H}{\lambda_H} \cosh \frac{d_N}{\lambda_N} \sinh \frac{d_H}{\lambda_H} }\end{align}$$ 系の幅を$W$とすると，逆スピンHall電圧は$V_{\text{3layer}} = E_y W$と書ける． よって $$\begin{align} V_{\text{3layer}} & = \frac{ 2 W \theta \sigma_H j_s^{(0)} }{\sigma_N d_N + \sigma_H d_H} \frac{ \sinh^2 \frac{d_H}{2 \lambda_H} }{ \frac{\sigma_N}{\lambda_N} \sinh \frac{d_N}{\lambda_N} \cosh \frac{d_H}{\lambda_H} + \frac{\sigma_H}{\lambda_H} \cosh \frac{d_N}{\lambda_N} \sinh \frac{d_H}{\lambda_H} } .\end{align}$$